Logic Puzzles with Prolog

Which language could be more suitable than Prolog for solving logic puzzles? (Answer: false.)

A vast array of interesting and commonly known logic puzzles can be elegantly and efficiently solved with Prolog and constraints. Some puzzles can be very directly modeled and solved as combinatorial tasks, others need more effort to find a suitable formulation as such tasks, and yet other puzzles require a search over different states. In the following, we consider a few example puzzles.

Knights and Knaves

For example, consider a few puzzles that appear in Raymond Smullyan's What Is the Name of This Book? and Maurice Kraitchik's Mathematical Recreations.

Video:

Premise: You are on an island where every inhabitant is either a knight or a knave. Knights always tell the truth, and knaves always lie.

Using Prolog and its CLP(B) constraints, we can model this situation as follows:

use 0 (false) to denote a knave
use 1 (true) to denote a knight
use one Boolean variable for each inhabitant, its truth value representing whether the person is a knave or a knight.

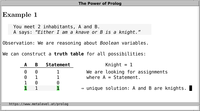
Example 1: You meet 2 inhabitants, A and B. A says: "Either I am a knave or B is a knight."

A single query over Boolean variables suffices to determine the kind of each inhabitant, by expressing the relation between A and the truth value of the statement:

?- sat(A =:= ~A+B).
   A = 1, B = 1.

This shows that both A and B are knights.

Example 2: A says: "I am a knave, but B isn't."

Translated to Boolean constraints, this corresponds to:

?- sat(A =:= ~A*B).
   A = 0, B = 0.

Thus, in this example, both A and B are knaves.

Example 3: A says: "At least one of us is a knave."

Using CLP(B) constraints, we can use the Boolean expression card(Ls,Exprs) to express a cardinality constraint: This expression is true iff the number of expressions in Exprs that evaluate to true is a member of the list Ls of integers. Thus, for this example, we can use:

?- sat(A =:= card([1,2],[~A,~B])).
   A = 1, B = 0.

Or, equivalently:

?- sat(A =:= ~A + ~B).
   A = 1, B = 0.

Example 4: You meet 3 inhabitants. A says: "All of us are knaves." B says: "Exactly one of us is a knight."

We can translate these two statements to a conjunction of constraints:

?- sat(A =:= (~A * ~B * ~C)), sat(B =:= card([1],[A,B,C])).
   A = 0, B = 1, C = 0.

Example 5: A says: "B is a knave." B says: "A and C are of the same kind." What is C?

We can translate this to Prolog as follows:

?- sat(A =:= ~B), sat(B =:= (A=:=C)).
   C = 0, clpb:sat(A=\=B).

This shows that C is definitely a knave. A and B can both be either knights or knaves, and they are of different kinds, which is indicated by the residual goal.

Which answer is correct?

Many other kinds of puzzles can be modeled by applying exactly the same method, i.e., reasoning over Boolean variables. Consider for example:

Which answer is correct?

All of the below.
None of the below.
All of the above.
At least one of the above.
None of the above.
None of the above.

Again, we can trivially translate this puzzle to statements over propositional logic. For example, let us use the Boolean variables A₁, A₂, ..., A₆ to denote whether or not the corresponding answer is selected. Then the different statements can be translated to relations over Boolean formulas as follows:

solution([A1,A2,A3,A4,A5,A6]) :-
        sat(A1 =:= A2*A3*A4*A5*A6),
        sat(A2 =:= ~(A3+A4+A5+A6)),
        sat(A3 =:= A1*A2),
        sat(A4 =:= A1+A2+A3),
        sat(A5 =:= ~(A1+A2+A3+A4)),
        sat(A6 =:= ~(A1+A2+A3+A4+A5)).

In this formulation, we are again assuming that your Prolog system ships with a dedicated constraint solver over Boolean domains that implements sat/1 as it is used above. For example, in SICStus Prolog and Scryer Prolog, such a solver is available as library(clpb).

The following interaction shows that only a single answer (option 5) can be selected in such a way that all statements are consistent.

?- solution(Vs).
   Vs = [0,0,0,0,1,0].

The Prolog system has automatically deduced the single admissible answer via constraint propagation.

Lewis Carroll

Lewis Carroll was a logic teacher who also published many entertaining puzzles.

In many of these puzzles, your job is to string together all given statements so that they form a chain of implications, typically arriving at a result that is surprising or amusing. For example:

None of the unnoticed things, met with at sea, are mermaids.
Things entered in the log, as met with at sea, are sure to be worth remembering.
I have never met with anything worth remembering, when on a voyage.
Things met with at sea, that are noticed, are sure to be recorded in the log.

Once more, we can translate each of these statements to a formula of propositional logic, but this time it is not so straight-forward because the language is intentionally a bit obfuscated. We make the simplifying assumption that all entities mentioned are met with at sea, since this qualification occurs, albeit cryptically, in each of the statements. Let us use the following abbreviations:

N	it is noticed
M	it is a mermaid
L	it is entered in the log
R	it is worth remembering
I	I have seen it

Using these abbreviations, we can model the puzzle as follows:

sea([N,M,L,R,I]) :-
        sat(M =< N),   % statement 1
        sat(L =< R),   % statement 2
        sat(I =< ~R),  % statement 3
        sat(N =< L).   % statement 4

It only remains to find a chain of implications that links all statements or their negations:

implication_chain([], Prev) --> [Prev].
implication_chain(Vs0, Prev) --> [Prev],
        { select(V, Vs0, Vs) },
        (   { taut(Prev =< V, 1) } -> implication_chain(Vs, V)
        ;   { taut(Prev =< ~V, 1) } -> implication_chain(Vs, ~V)
        ).

Sample query:

?- sea(Vs),
   Vs = [N,M,L,R,I],
   select(Start, Vs, Rest),
   phrase(implication_chain(Rest, Start), Cs).

In this case, the two solutions for Cs are: [M,N,L,R,~I] and [I,~R,~L,~N,~M]. Informally, this translates to "If it is a mermaid, I have not seen it", and "If I have seen it, it is not a mermaid", respectively. The whole chain, in the first case, is: If it is a mermaid, it is noticed, hence it is entered in the log, hence it is worth remembering, hence I have not seen it. Informally, the "solution" of this puzzle is: I have never seen a mermaid.

Such deductions also frequently arise or are needed when applying Prolog for theorem proving.

Cryptoarithmetic puzzles

Cryptoarithmetic puzzles require us to find digits corresponding to letters or symbols, such that the represented numbers satisfy certain constraints.

An example of a cryptoarithmetic puzzle is:

      CP
+     IS      
+    FUN
--------
=   TRUE

Different letters correspond to different digits.

Integer constraints are a great fit for such puzzles. Let us first define the relation between a list of digits and the represented number:

digits_number(Ds, N) :-
        length(Ds, _),
        Ds ins 0..9,
        reverse(Ds, RDs),
        foldl(pow, RDs, 0-0, N-_).

pow(D, N0-I0, N-I) :-
        N #= N0 + D*10^I0,
        I #= I0 + 1.

Using digits_number/2 as a building block, we can ask for solutions with:

?- digits_number([C,P], CP),
   digits_number([I,S], IS),
   digits_number([F,U,N], FUN),
   digits_number([T,R,U,E], TRUE),
   CP + IS + FUN #= TRUE,
   Vs = [C,P,I,S,F,U,N,T,R,E],
   all_distinct(Vs),
   label(Vs).

The first solution is: 12+83+579=674. On backtracking, all solutions are generated. We can easily express further constraints. For example, we can generate solutions where T is not 0 by adding the constraint T#\=0. This yields the solution 23+74+968=1065.

Zebra Puzzle

There is a well-known puzzle commonly known as Zebra Puzzle.

Let us consider the following variant of this famous group of puzzles:

Zebra Puzzle: There are five houses, each painted in a unique color. Their inhabitants are from different nations, own different pets, drink different beverages and smoke different brands of cigarettes.

The Englishman lives in the red house.
The Spaniard owns the dog.
Coffee is drunk in the green house.
The Ukrainian drinks tea.
From your perspective, the green house is immediately to the right of the ivory house.
The Old Gold smoker owns snails.
Kools are smoked in the yellow house.
Milk is drunk in the middle house.
The Norwegian lives in the first house.
The man who smokes Chesterfields lives in the house next to the man with the fox.
Kools are smoked in the house next to the house where the horse is kept.
The Lucky Strike smoker drinks orange juice.
The Japanese smokes Parliaments.
The Norwegian lives next to the blue house.

Who drinks water? Who owns the zebra?

Such puzzles can be very conveniently solved by first translating the entities to integers, and then using your Prolog system's declarative integer arithmetic to state the given hints as relations between variables whose domains are sets of integers. For example, if the position of a house is represented as a variable H with domain {1,2,3,4,5}, then the following relation holds for any neighbouring house N:

abs(H-N) #= 1

This relation works correctly in all directions, no matter which of the two variables, if any, is already instantiated. Thus, translating such puzzles to integers often increases convenience when expressing the desired relations, and often also improves performance due to pruning techniques that are automatically applied. In addition, keeping your programs pure lets you benefit from powerful additional techniques such as declarative debugging.

Thus, let us consider the following Prolog formulation of the task:

solution(Pairs, Water, Zebra, Vs) :-
        Table   = [Houses,Nations,Drinks,Smokes,Animals],
        Houses  = [Red,Green,Yellow,Blue,Ivory],
        Nations = [England,Spain,Ukraine,Norway,Japan],
        Names   = [england,spain,ukraine,norway,japan],
        Drinks  = [Coffee,Milk,OrangeJuice,Tea,Water],
        Smokes  = [OldGold,Kools,Chesterfield,LuckyStrike,Parliaments],
        Animals = [Dog,Snails,Horse,Fox,Zebra],
        pairs_keys_values(Pairs, Nations, Names),
        maplist(all_distinct, Table),
        append(Table, Vs),
        Vs ins 1..5,
        England #= Red,               % hint 1
        Spain #= Dog,                 % hint 2
        Coffee #= Green,              % hint 3
        Ukraine #= Tea,               % hint 4
        Green #= Ivory + 1,           % hint 5
        OldGold #= Snails,            % hint 6
        Kools #= Yellow,              % hint 7
        Milk #= 3,                    % hint 8
        Norway #= 1,                  % hint 9
        next_to(Chesterfield, Fox),   % hint 10
        next_to(Kools, Horse),        % hint 11
        LuckyStrike #= OrangeJuice,   % hint 12
        Japan #= Parliaments,         % hint 13
        next_to(Norway, Blue).        % hint 14

next_to(H, N) :- abs(H-N) #= 1.

Using labeling, we obtain the puzzle's unique solution:

?- solution(Pairs, Water, Zebra, Vs), label(Vs).
   Pairs = [3-england,4-spain,2-ukraine,1-norway,5-japan],
   Water = 1,
   Zebra = 5,
   Vs = [3,5,1,2,4,3,4,2,1,5,5,3,4,2,1,3,1,2,4,5|...]
;  false.

Dozens of questions on Stackoverflow are about solving this famous puzzle or closely related ones with Prolog. You can thus read the existing questions and answers for more information.

Wolf and Goat etc.

Another group of famous puzzles are known as river crossing puzzles. Again, such puzzles can be modeled in Prolog in a straight-forward way, by describing the different states of all entities, and formulating relations between these states. You can use Prolog's built-in search strategy to search for a sequence of admissible state transitions that let you reach the desired target state. Use iterative deepening to find a shortest solution. In Prolog, you can easily obtain iterative deepening via length/2, which creates lists of increasing length on backtracking.

See Escape from Zurg for one interesting example.

More about Prolog

Main page