Higher-order Predicates
Prolog predicates that take predicates as arguments are
called higher-order predicates, or meta-predicates.
| Video: |
|
call/N
The call/N family
of built-in predicates allow us to
call Prolog partial goals
dynamically. A partial goal is a term that denotes a
Prolog goal to which zero or more arguments are added before it is
called.
The mechanism to invoke arbitrary Prolog goals dynamically is
called meta-call, and it is the basic building block by
which we can define arbitrary meta-predicates in Prolog.
Importantly, the call/N family of predicates
retain logical purity of the
predicates they call.
Like most meta-predicates, call/N could
in principle be implemented in Prolog itself. For
example, we could implement call/1 as follows, using one
clause for each available predicate:
call(true).
call(X #= Y) :- X #= Y.
call(call(G)) :- call(G).
etc.
Of course, this would need an impractical number of clauses
in practice, and for this reason the call/N family
of predicates is implemented differently.
maplist/N
The predicates maplist/2 and maplist/3 are among
the most important and most frequently used meta-predicates. All
widely used Prolog systems provide them as built-in or library
predicates.
The goal maplist(Pred_1, Ls) is true
iff call(Pred_1, L) is true for each
element L in the list Ls.
The goal maplist(Pred_2, As, Bs) is true
iff call(Pred_2, A, B) is true for each pair of
elements A∈As
and B∈Bs that have the same index.
There are further predicates in this family
(maplist/[4,5,...]) that are less frequently used.
If your Prolog system does not provide these predicates, you can
easily define them yourself. For example, maplist/3 is
declaratively equivalent to:
maplist(_, [], []).
maplist(Pred_2, [A|As], [B|Bs]) :-
call(Pred_2, A, B),
maplist(Pred_2, As, Bs).
Using goal expansion, the meta-call can
be compiled away in many cases to improve performance.
The primary advantage of maplist/N is that you can lift
any relation that holds for a single element (or single
pair, triple, etc. of elements) to lists of such elements
(or corresponding elements).
For example, we can state that a term E
is different from all elements in Ls:
?- maplist(dif(E), Ls).
Ls = []
; Ls = [_A], dif:dif(E,_A)
; Ls = [_A,_B], dif:dif(E,_A), dif:dif(E,_B)
; Ls = [_A,_B,_C], dif:dif(E,_A), dif:dif(E,_B), dif:dif(E,_C)
; ... .
This works in all directions, even if Ls is not
instantiated.
if_/3 and related predicates
The meta-predicate if_/3 is an important recent
development that is described
in Indexing
dif/2 by Ulrich Neumerkel and Stefan Kral.
Implementations are available for:
- SICStus Prolog: library(reif)
- Scryer Prolog ships with library(reif). Post ?- use_module(library(reif)). to use if_/3 and related meta-predicates.
- SWI-Prolog: library(reif)
Importantly, if_/3 combines desirable declarative
properties with good performance in many situations of high
practical relevance.
For example, the predicate hailstone/2 that is described
in Basic Concepts can be
expressed with if_/3 as follows:
hailstone(N, N).
hailstone(N0, N) :-
R #= N0 mod 2,
if_(R = 0,
N0 #= 2*N1,
N1 #= 3*N0 + 1),
hailstone(N1, N).
if_/3 correctly commits to one of the two alternatives
when admissible and retains full generality.
See also the predicates tfilter/3, tpartition/4 and
other features that are provided by this important new library.
foldl/N
The foldl/N family of predicates describe a fold from
the left of a list. You can think of a fold as a list
traversal with intermediate states. An intermediate state
becomes final when no more elements remain.
The most frequently used of these predicates
is foldl/4:
foldl(Pred_3, Ls, S0, S) describes a fold from the left
of the list Ls, where S0 is the initial state
and S is the final state. For each
element L∈Ls and intermediate
state Sn, call(Pred_3, L,
Sn, Sn+1) is invoked to relate the
current list element L and intermediate
state Sn to the next intermediate
state Sn+1.
Again, these predicates let us focus on the relation for one
element at a time, and then lift this relation to lists of
elements.
For example, consider the following relation between two integers
and their sum:
integer_integer_sum(A, B, S) :- S #= A + B.
Using this relation, we can express the sum of
a list Ls of integers with foldl/4,
using 0 as the initial state:
?- foldl(integer_integer_sum, Ls, 0, S).
Ls = [], S = 0
; Ls = [S], clpz:(S in inf..sup)
; Ls = [_A,_B], clpz:(_B+_A#=S)
; Ls = [_A,_B,_C], clpz:(_B+_A#=_J), clpz:(_C+_J#=S)
; ... .
As another example, we can define the maximum of a
list Ls of integers as follows:
list_maximum([L|Ls], Max) :- foldl(maximum_, Ls, L, Max).
maximum_(A, B, Max) :- Max #= max(A, B).
In this case, we use the first element of the list as the initial state.
All solutions predicates
There are several built-in predicates that let us obtain all
solutions of a predicate.
These predicates transform solutions that are normally found on
backtracking to lists of solutions. The former is sometimes
called a temporal representation, and the latter
a spatial representation.
The most important such predicates
are bagof/3, setof/3
and findall/3.
In general, reasoning about the database in this way
destroys monotonicity of your programs: After adding
a clause, goals that previously succeeded may fail if
these predicates are used. This may
render declarative debugging approaches
inapplicable. One way to see why these predicates are problematic
is to observe that (\+)/1 ("not provable") can be
implemented via findall/3:
\+ Goal :- findall(., Goal, []).
For this reason, use these predicates with caution.
Further reading
Ulrich
Neumerkel's library(lambda)
is an important recent proposal for
lambda expressions in ISO Prolog. Use this
library in cases where you would like to call variations of
predicates without introducing auxiliary predicates.
Richard O'Keefe's
draft, An
Elementary Prolog Library, also contains descriptions and
implementations for many important higher-order predicates.
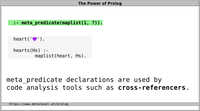
meta_predicate declarations provide sufficient
type information to make code analysis tools such as
cross-referencers work with meta-predicates.
| Video: |
|
More about Prolog
Main page


