Solving Sudoku with Prolog

Prolog solution

Prolog is extremely well suited for solving combinatorial tasks like Sudoku.

Video:

For example, using CLP(ℤ) constraints, a valid Sudoku board can be concisely expressed like this:

sudoku(Rows) :-
        length(Rows, 9),
        maplist(same_length(Rows), Rows),
        append(Rows, Vs), Vs ins 1..9,
        maplist(all_distinct, Rows),
        transpose(Rows, Columns),
        maplist(all_distinct, Columns),
        Rows = [As,Bs,Cs,Ds,Es,Fs,Gs,Hs,Is],
        blocks(As, Bs, Cs),
        blocks(Ds, Es, Fs),
        blocks(Gs, Hs, Is).

blocks([], [], []).
blocks([N1,N2,N3|Ns1], [N4,N5,N6|Ns2], [N7,N8,N9|Ns3]) :-
        all_distinct([N1,N2,N3,N4,N5,N6,N7,N8,N9]),
        blocks(Ns1, Ns2, Ns3).

Like all pure Prolog programs, this predicate can be used in all directions. You can use it to:

complete partial squares
test complete squares
generate all Sudoku Latin squares.

For example, we can use the code to generate valid Sudoku boards:

      ?- sudoku(Rows), maplist(label, Rows), maplist(portray_clause, Rows).
      [1,2,3,4,5,6,7,8,9].
      [4,5,6,7,8,9,1,2,3].
      [7,8,9,1,2,3,4,5,6].
      [2,1,4,3,6,5,8,9,7].
      [3,6,5,8,9,7,2,1,4].
      [8,9,7,2,1,4,3,6,5].
      [5,3,1,6,4,2,9,7,8].
      [6,4,2,9,7,8,5,3,1].
      [9,7,8,5,3,1,6,4,2].
         Rows = [[1,2,3,4,5,6,7,8,9]|...]

A partial instantiation of the rows turns this into a completion task, which is what we commonly understand as a Sudoku puzzle.

Source file

Prolog source file: sudoku.pl

The source file contains:

the Prolog formulation of Sudoku puzzles which is shown above
PostScript instructions for showing animations of the search process
sample Sudoku instances, available is problem/2.

You can try it with Scryer Prolog:

      $ scryer-prolog sudoku.pl

Sample query and answer:

      ?- problem(1, Rows),
         sudoku(Rows),
         maplist(labeling([ff]), Rows),
         maplist(portray_clause, Rows).
      [1,5,6,8,9,4,3,2,7].
      [9,2,8,7,3,1,4,5,6].
      [4,7,3,2,6,5,9,1,8].
      [3,6,2,4,1,7,8,9,5].
      [7,8,9,3,5,2,6,4,1].
      [5,1,4,9,8,6,2,7,3].
      [8,3,1,5,4,9,7,6,2].
      [6,9,7,1,2,3,5,8,4].
      [2,4,5,6,7,8,1,3,9].
         Rows = [[1,5,6,8,9,4,3,2,7]|...]

Animations

If you have the PostScript viewer "gs" installed, you can view an animation of the constraint solving process.

Sample PostScript file, a self-contained saved animation for a Sudoku puzzle (open it with "gv" or "gs" to view it): solved.ps.gz

Here is a shell command that you can try, using show/2 to animate the search:

      $ scryer-prolog -g 'problem(1,Rows),show([ff],Rows)' sudoku.pl | \
           gs -dNOPROMPT -g680x680 -dGraphicsAlphaBits=2 -r150 -q

The arguments of show/2 are:

a list of labeling options
a list of 9 rows that are to be completed to a Sudoku Latin square. Each row is a list of 9 variables, which can also be already instantiated to integers to fill in initial elements.

As a side-effect, you see an animation of the constraint solving process. To make the search more interesting, you can replace all_distinct/1 with the weaker constraint all_different/1 in the source file.

Here's an intermediate state:

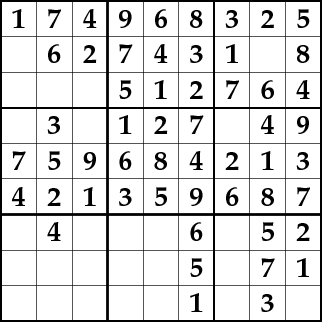
And here is a picture of a finished animation:

Further reading: Neumerkel at al., Visualizing Solutions with Viewers.

More CLP(ℤ) examples: https://github.com/triska/clpz

More about Prolog: The Power of Prolog

Main page